
Kuchtacht via Wikimedia
The twisted math of knot theory can help you tell an overhand knot from an unknot
It's knot always easy to tell if two knots are the same
Could atoms really be knots tied in a mysterious substance called ether?
That was the theory proposed in the 1860s by British physicist Lord Kelvin. While we now know that his theory is not correct, Kelvin's idea inspired the Scottish physicist and mathematician Peter Guthrie Tait to create a “table of the elements” by making a table of knots. Tait was not the only one tabulating knots. Reverend Thomas Kirkman, a British mathematician and minister, and Charles Little, an American mathematician, got in on the fun, too. And so began the rise of the mathematical field known as knot theory.
Unsurprisingly, mathematical knots are pretty similar to knots from everyday life. Suppose we take a long piece of rope or string, tie a knot in the middle, and then stick the ends together so that they are not loose. A mathematical knot is then "just such a knotted loop of string, except that we think of the string as having no thickness, its cross-section being a single point".
The "unknot" and the trefoil knot are the two simplest examples of mathematical knots. To make an unknot, simply take your piece of rope or string and glue its ends together, without tying a knot in the middle. To make the trefoil knot, first make an overhand knot and then glue its ends together.

An unknot (left) and a trefoil knot (right)
Via Wikimedia
We can represent both of these knots, and any other kind, by using a special kind of diagram called, well, a knot diagram. Think of these diagrams as capturing a knot’s shadow on the wall. For example, the image below shows a table of knots that have up to seven crossings, which are places where strands of the knot cross. At a crossing we leave a little bit of space in the diagram to indicate which strand goes underneath and which stays on top. The diagram for the unknot is on the top left and is drawn with zero crossings, while the diagram for the trefoil knot is next to it on the right and is drawn with three crossings.
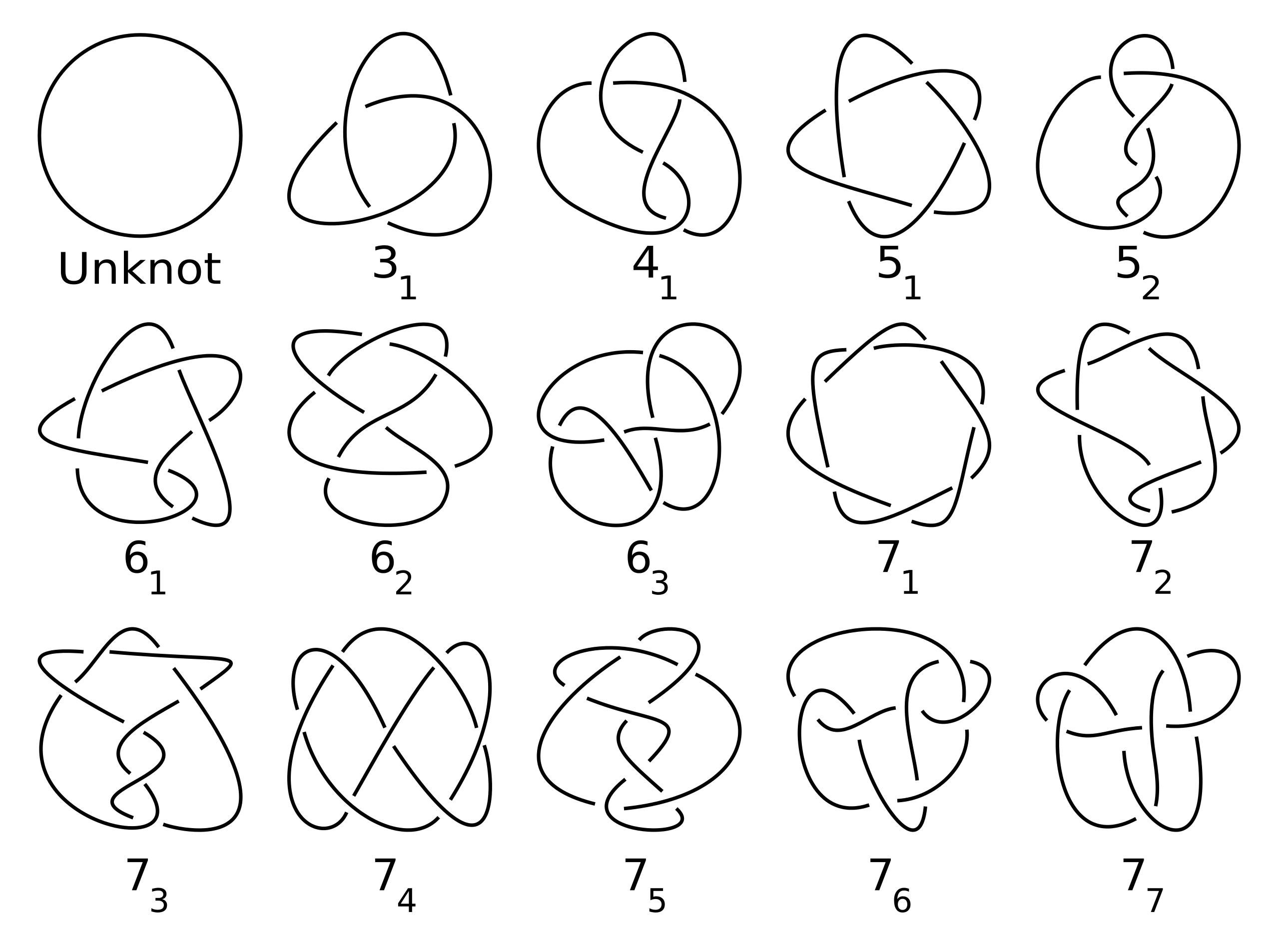
A table of knots with up to seven crossings. The knot on the top left is the unknot and the knot immediately to its right is the trefoil knot
Via Wikimedia
An important question in knot theory is: how can we tell if two knots are the same? Intuitively, two knots are the same when we can turn one into the other by wiggling it around but without breaking it. Thanks to the German mathematician Kurt Reidemeister, we can show two knots are the same by working with knot diagrams. Reidemeister proved that two knots are the same if and only if we can turn a diagram of one into a diagram of the other by using a sequence of simple moves known as Reidemeister moves.
There are only three types of these moves. The first, called the Reidemeister type I move, allows you to add in or remove a twist to the diagram. The Reidemeister type II move allows you to add or take away two crossings. The third and final move, the Reidemeister type III move, allows you to move a strand in the knot diagram from one side of a crossing to the other.
The knot diagram below looks different to the diagram of the unknot that we saw earlier, but we can use Reidemeister moves to show that they represent the same knot. We just need to apply a type I Reidemeister move twice, to each of its twists, and we get back the familiar diagram of the unknot we saw earlier.
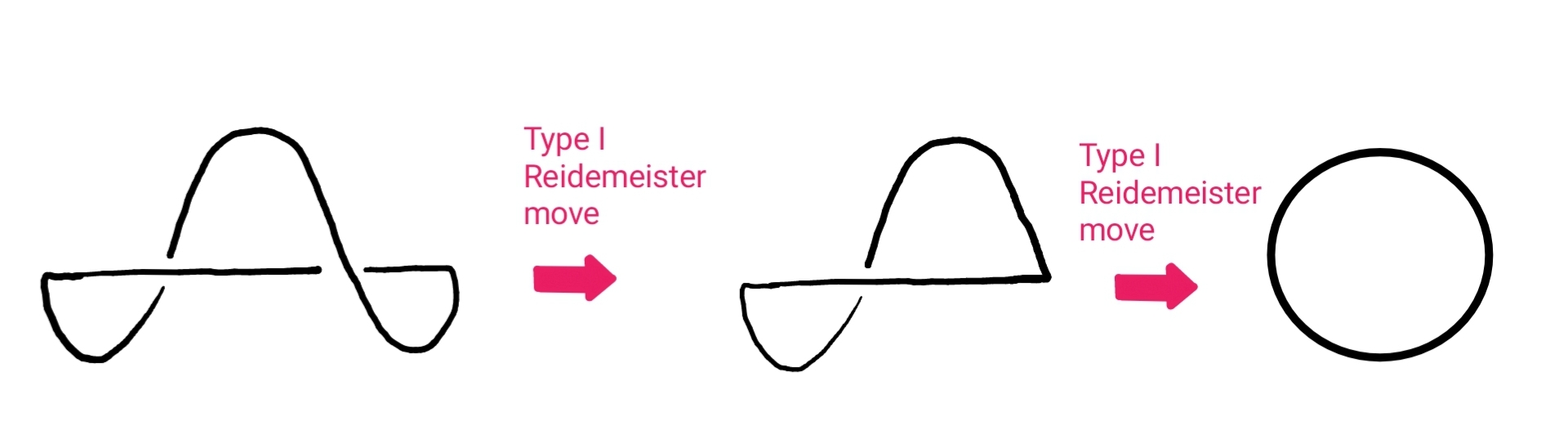
By applying a type I Reidemeister move twice, we can turn the knot diagram on the left into the diagram of the unknot we saw earlier
Rebecca Lea Morris
While that example was quite simple, in general trying to figure out if two knots are the same using Reidemeister moves is “pretty much impossible” says Jessica Purcell, professor of mathematics at Monash University. The problem, she explained via email, is that when trying to show two knots are the same “you can play around with Reidemeister moves and maybe you’ll magically move one into the other. But if you don’t, there’s no way to know if you can’t because the knots are different, or if you just haven’t found the right moves and need to keep trying.”
The difficulty of showing two knots are the same is illustrated by the story of the "Perko Pair" of knots. Charles Little thought that these knots were distinct and listed them as separate entries in one of his knot tables in 1899. John Conway checked Little’s table in the 1960s and didn’t notice anything suspicious about them. But in 1973 lawyer and mathematician Kenneth Perko "sketched a few diagrams to see if they might be the same" and found "a page and a half of yellow legal pad later" that they were. His short paper gave an abbreviated set of diagrams indicating how they could be transformed into each other. Perko’s discovery had important consequences by showing that a “theorem” Little thought he had proved was incorrect.
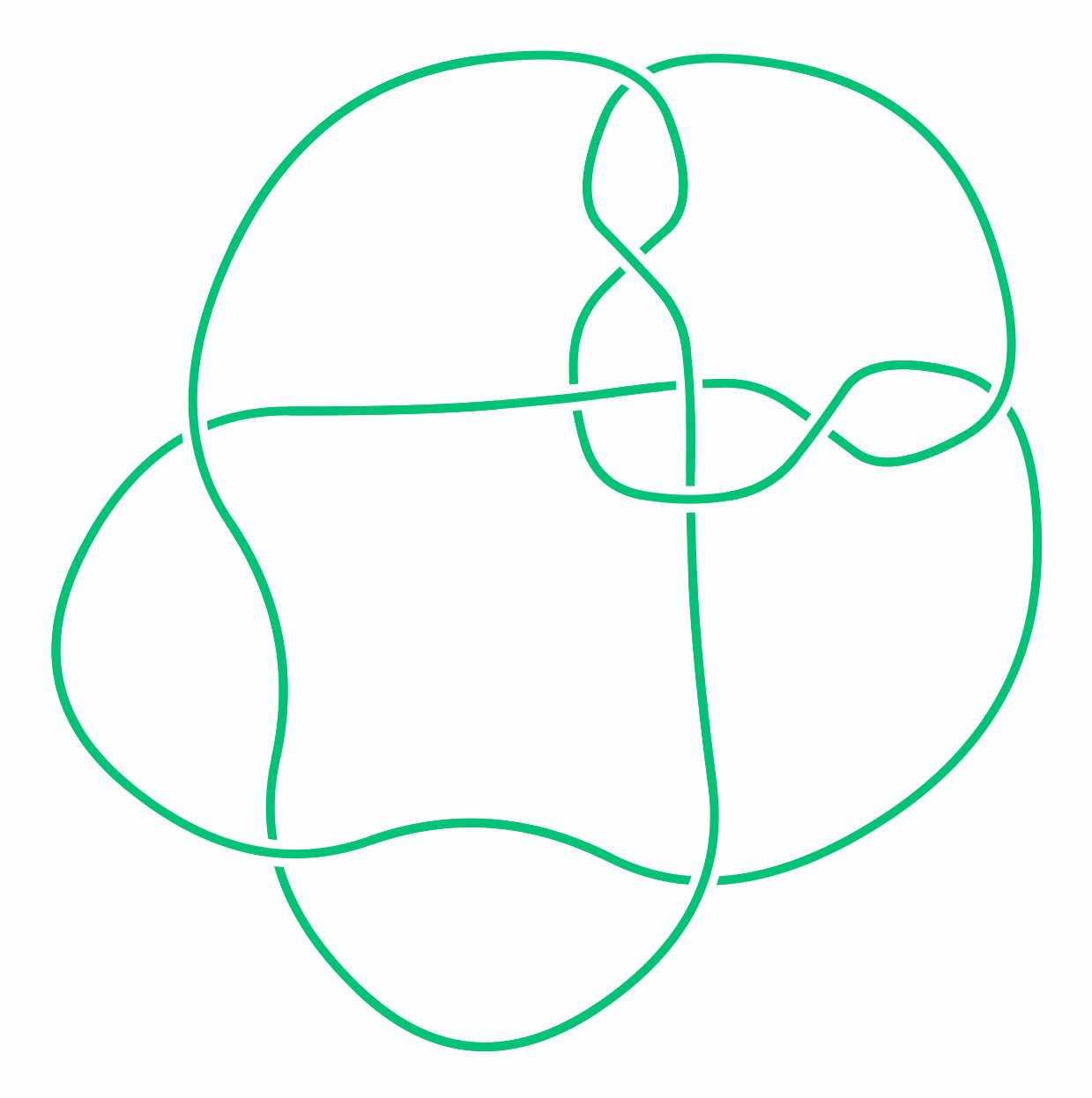
A knot diagram representing the first of the “Perko Pair” of knots
Via Wikimedia
While it might seem shocking that the mistake about the Perko Pair went undetected for 74 years, Purcell doesn’t think it is too surprising. “After moving diagrams around for a long time, and finding no moves to turn one into the other, it makes sense that [early knot theorists] might give up and declare the knots to be different,” she said.
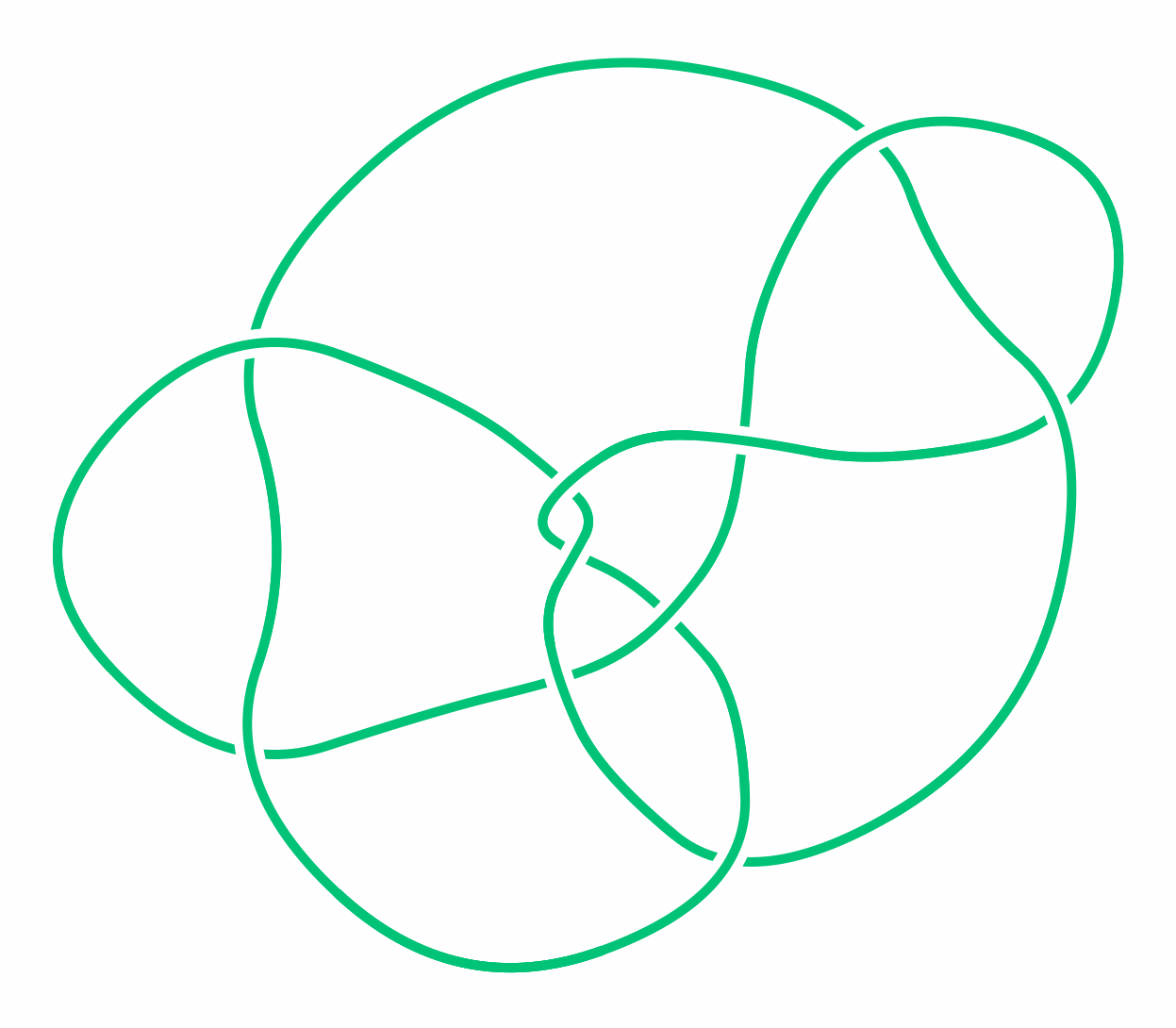
A knot diagram representing the second of the “Perko Pair” of knots. See? Clearly the same as the first
Via Wikimedia
Now, however, mathematicians have a way to actually prove that two knots are different: tools called knot invariants. Imagine that we match up each knot with a label that has something written on it, such as a word or a number. This matching of knots to labels is called a "knot invariant" if equivalent knots, like the Perko pair, have the same label. To prove that two knots really are different, we need to find a type of knot invariant that matches those knots to labels that say different things.
As an example, consider a matching where a knot's label can say either "tricolorable" or "not tricolorable." A knot is assigned the "tricolorable" label when we can color each strand in its diagram one of three colors, say blue, red or green, while making sure that two conditions are met.
The first condition is that we must use at least two colors in the diagram (which, yes, is confusing when talking about "tri"colorability). The second is that, at each crossing, the three strands must either all be the same color or all be different colors. The trefoil gets assigned the "tricolorable" label because we can color it according to these rules, as depicted in the diagram.
On the other hand, if we cannot color a knot's diagram in this way then it gets assigned the "not tricolorable" label. The unknot, for example, is assigned the "not tricolorable" label because no matter how we try to color it, we can only use one color because it only has one arc to color, but we need to use at least two for a knot to be tricolorable. The matching of knots to the labels of "tricolorable" or "not tricolorable" is a knot invariant. So as we've seen that the trefoil is assigned "tricolorable" and the unknot is assigned "not tricolorable," this proves that they really are different knots.

A tricoloring of the trefoil knot
Via Wikimedia
Knot invariants are the topic of cutting edge research. Purcell explains that mathematicians find them “arising from many different places, including geometry, algebra and physics” and are trying to understand the connections between them.
She added, “I think some of the most exciting questions in knot theory right now involve how certain quantum invariants arising from physics relate to other information about knots arising from geometry.” In addition to physics, knot theory also has connections to biology and chemistry. DNA, for example, gets knotted and cut up into pieces by enzymes and knot theory can help scientists understand how this all works. In chemistry, knot theory can be applied to help scientists create knotted molecules. So while knot theory did not lead to a “table of the elements” like Lord Kelvin and Tait had hoped, it does have exciting links to physics, chemistry and biology.



Wow – that was a very interesting read Rebecca, and I have newfound respect for hair-bands now! It is impressive how you managed to make some really advanced concepts in Knot theory easy to follow, especially for non-mathematicians. Is there a theory that describes everyday knots, specifically knots that have loose ends (like shoelaces)? Understanding how loose fibers entangle can have implications in composite materials, especially when fiber reinforcements are used.